The Different Views of Probability
Four hundred years of scientific research and the broad acceptance of a formal axiom system have not brought a common agreement on the philosophical foundations of probability theory. Instead, many different interpretations have arisen during this time, and none has succeeded in putting an end to the discussion about what probability really is. The interested reader will find an excellent account of the historical development of the competing theories in Hacking (1975), while valuable comparative studies can be found in the works of Fine (1973), Weatherford (1982), and Cohen (1989).
The classical approach regards probability as the ratio of favorable cases to total, equipossible cases (Laplace, 1996/1826; Ball, 2003/1908). The logical approach regards probability as a logical relation between statements of evidence and hypothesis (Carnap, 1950; Keynes, 2004/1921). The frequentist view regards probability as the limiting frequency of successful outcomes in a long sequence of trials (von Mises, 1981/1928). The propensity view (Popper, 1957, 1959; Hacking, 1965; Lewis, 1980) regards probability as a physical tendency for certain events to occur. Finally, the subjectivist school understands probability as the degree of belief of an ideal rational agent about hypotheses for which the truth-value is unknown (Ramsey, 1931; Savage, 1972/1954; de Finetti, 1974). Despite the differences in philosophical interpretation, the mathematics is common to all approaches.
PR-OWL is related to the task of representing uncertain, incomplete knowledge that can come from diverse agents. For this reason, it abides to the subjectivist view of probability. The choice of subjective probability as PR-OWL's representation for uncertainty was made because of its status as a mathematically sound representation language and formal calculus for rational degrees of belief, and because it gives different agents the freedom to have different beliefs about a given hypothesis.
Although the interpretation taken here is subjectivist, the methodology is consistent with other interpretations of probability. For example, some might prefer a frequency or a propensity interpretation for probabilities that arise from processes considered to be intrinsically random. Such individuals would naturally build probabilistic ontologies only for processes they regard as intrinsically random. Others might prefer a logical interpretation of a probabilistic domain theory. In the end, the above-mentioned discussion of what probability “really is” may be better framed as an argument over what kind of applications would render justifiable the use of a probabilistic axiom system and its underlying mathematics.
Many different axiomatic formulations have been proposed that give rise to subjectivist probability as a representation for rational degrees of belief. Examples include the axiom systems of Ramsey (1931), Kolmogorov (1960/1933), Cox (1946), Savage (1972/1954), and De Finetti (de Finetti, 1990/1974). As an illustration, the following axiom system is due to Watson & Buede (1987):
- For any two uncertain events, A is more likely than B, or B is more likely than A, or they are equally likely.
- If A1 and A2 are any two mutually exclusive events, and B1 and B2 are any other mutually exclusive events; and if A1 is not more likely than B1, and A2 is not more likely than B2; then (A1 and A2) is not more likely than (B1 and B2). Further, if either A1 is less likely than B1 or A2 is less likely than B2, then (A1 and A2) is less likely than (B1 and B2).
- A possible event cannot be less likely than an impossible event.
- Suppose A1, A2, … is an infinite decreasing sequence of events; that is , if Ai occurs, then Ai-1 occurs, for any i. Suppose further that Ai is not less likely than some other event B, again for any i. Then the occurrence of all the infinite set of events Ai, I = 1,2,…, , is not less likely than B.
- There is an experiment, with a numerical outcome, such that each possible value of that outcome, in a given range, is equally likely.
All the properties of the probabilistic system used by Bayesian Networks, Influence Diagrams, MEBN, and PR-OWL can be derived from those axioms. Among those, two transformations are crucial for the notion of probabilistic inference: the Law of Total Probability and the Bayes Rule.
The Law of Total Probability and the Bayes Rule
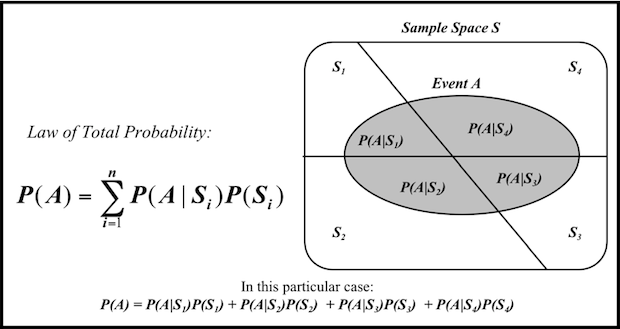
The Law of Total Probability, also known as multiplicative law (Page, 1988, page 17), gives the marginal probability distribution of a subset of random variables from joint distribution on a superset by summing over all possible values of the random variables not contained in the subset. The figure below illustrates the concept.
Bayes rule, also known as Bayes theorem, was devised in by Thomas Bayes more than two centuries ago and provides a method of updating the probability of a random variable when information is acquired about a related random variable. The standard format of Bayes rule is:
P(B) is called prior probability of B, as it reflects our belief in event B before obtaining information on event A. Likewise, P(B|A) is the posterior probability of B, and represents our new belief on event B after applying Bayes rule with the information collected from event A.
Bayes rule provides the formal basis for the active and rapidly evolving field of Bayesian probability and statistics. In the Bayesian view, inference is a problem of belief dynamics. Bayes rule provides a principled methodology for belief change in the light of new information.
Good introductory material on Bayesian Statistics can be found in works of Press (1989), Lee (2004), and Gelman (2003), while a more philosophically oriented reader will be also interested in the collection of essays on foundational studies in Bayesian decision theory and statistics by Kadane et al. (1999). The above concepts provide the formal mathematical basis for the most widely used Bayesian Inference technique today: Bayesian Networks