Recursive MFrags
The figure below represents the recursive MFrag ZoneMD of the Starship model. There, the magnetic disturbance of given zone at a time t is dependent upon the magnetic disturbance observed during its previous iteration (time t-1). A careful reading of the context nodes will make it clear that in order for the local distribution to apply, z has to be a zone and st has to be a starship that has z as its current position. In addition, tprev and t must be TimeStep entities, and tprev is the step preceding t..

Other varieties of recursion can also be represented in MEBN logic by means of MFrags that allow influences between instances of the same random variable. Allowable recursive definitions must ensure that no random variable instance can influence its own probability distribution. General conditions that both recursive and non-recursive MFrags and MTheories must satisfy are given in Laskey (2005).
As in non-recursive MFrags, the input nodes in a recursive MFrag include nodes whose local distributions are defined in another MFrag (i.e., CloakMode(st)). In addition, the input nodes may include instances of recursively-defined nodes in the MFrag itself. For example, the input node ZoneMD(z, tprev) represents the magnetic disturbance in zone z at the previous time step, which influences the current magnetic disturbance ZoneMD(z, t). The recursion is grounded by specifying an initial distribution at time !T0 that does not depend on a previous magnetic disturbance.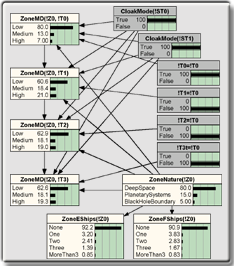
The figure on the right illustrates how recursive definitions can be applied to construct a situation-specific Bayesian Network (SSBN) to answer a query. In this specific case, the query concerns the magnetic disturbance at time !T3 in zone !Z0, where !Z0 is known to contain the uncloaked starship !ST0 (Enterprise) and exactly one other starship !ST1, which is known to be cloaked.
The process to build the graph shown in this picture begins by creating an instance of the home MFrag of the query node ZoneMD(!Z0,!T3). That is, !Z0 is substituted for z and !T3 for t, and then all instances of the remaining random variables that meet the context constraints are created. The next step is to build any conditional probability tables (CPTs) that can already be built on the basis of the available data. CPTs for ZoneMD(!Z0,!T3), ZoneNature(!Z0), ZoneEShips(!Z0), and ZoneFShips(!Z0) can be constructed because they are resident in the retrieved MFrag. Single-valued CPTs for CloakMode(!ST0), CloakMode(!ST1), and !T3=!T0 can be specified because the values of these random variables are known.
At end of the above process, only one node, ZoneMD(!Z0,!T2), remains for which there is no CPT. To construct its CPT, its home MFrag must be retrieved, and any random variables that meet its context constraints and have not already been instantiated must be instantiated. The new random variables created in this step are ZoneMD(!Z0,!T1) and !T2=!T0. The value of the latter is already known, while the home MFrag of the former has to be retrieved. This process continues until all the nodes of Figure 11 are added. At this point, the CPTs for all random variables can be constructed, and thus the SSBN is complete.
The MFrag depicted in the figure above defines the local distribution that applies to all these instances, even though for brevity only the probability distributions (local and default) for node ZoneMD(z, t) were displayed. The remaining distributions can be found in Appendix A. Note that when there is no starship with cloak mode activated, the probability distribution for magnetic disturbance given the zone nature does not change with time. When there is at least one starship with cloak mode activated, then the magnetic disturbance tends to fluctuate regularly with time in the manner described by the local expression. For the sake of simplicity, the underlying assumption that the local distribution depends only on whether there is a cloaked starship nearby was adopted, although in a more “realistic” model the disturbance might increase with the number of cloaked starships and/or the power of the cloaking device.
Another implicit assumption taken in this example regards the initial distribution for the magnetic disturbance when there are cloaked starships, which was assumed to be equal to the stationary distribution given the zone nature and the number of cloaked starships present initially. Of course, it would be possible to write different local expressions expressing a dependence on the number of starships, their size, their distance from the Enterprise, etc.
MFrags provide a flexible means to represent knowledge about specific subjects within the domain of discourse, but the true gain in expressive power is revealed when these “knowledge patterns” are aggregated in order to form a coherent model of the domain of discourse that can be instantiated to reason about specific situations and refined through learning.
It is important to note that just collecting a set MFrags that represent specific parts of a domain is not enough to ensure a coherent representation of that domain. For example, it would be easy to specify a set of MFrags with cyclic influences, or one having multiple conflicting distributions for a random variable in different MFrags. In order to define complete and coherent domain models as collections of MFrags, one needs to understand the concept of MTheories.