Basics of MFrags
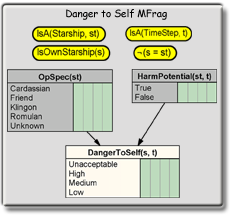
Like a BN, an MFrag contains nodes, which represent RVs, arranged in a directed graph whose edges represent direct dependence relationships. An isolated MFrag can be roughly compared with a standard BN with known values for its root nodes and known local distributions for its non-root nodes. For example, the MFrag depicted below was taken from a MEBN model on the Star Trek domain, and represents knowledge about the degree of danger to which one's starship is exposed. The fragment graph has seven nodes. The four nodes at the top of the figure are context nodes; the two shaded rectangular nodes below the context nodes are the input nodes; and the bottom node is a resident node.
A node in an MFrag may have a parenthesized list of arguments. These arguments are placeholders for entities in the domain. For example, the argument st to HarmPotential(st, t) is a placeholder for an entity that has a potential to harm, while the argument t is a placeholder for the time step this instance represents. To refer to an actual entity in the domain, the argument is replaced with a unique identifier. By convention, unique identifiers begin with an exclamation point, and no two distinct entities can have the same unique identifier. The result of substituting unique identifiers for a RV’s arguments is one or more instances of that RV. For example, HarmPotential(!ST1, !T1) and HarmPotential(!ST2, !T1) are two instances of HarmPotential(st, t) that both occur in the time step !T1.
The resident nodes of an MFrag have local distributions that define how their probabilities depend on the values of their parents in the fragment graph. In a complete MTheory, each random variable has exactly one home MFrag, where its local distribution is defined. Input and context nodes (e.g., OpSpec(st) or IsOwnStarship(s)) influence the distribution of the resident nodes, but their distributions are defined in their own home MFrags.
Context nodes represent conditions that must be satisfied for the influences and local distributions of the fragment graph to apply. Context nodes may have value True, False, or Absurd. Context nodes having value True are said to be satisfied. As an example, if the unique identifier for the Enterprise (i.e., !ST0) is substituted for the variable s in IsOwnStarship(s), the resulting hypothesis will be true. If, instead, a different starship unique identifier (say, !ST1) is used, then this hypothesis will be false. Finally, if the unique identifier of a non-starship (say, !Z1) replaces s, then this statement is absurd (i.e., it is absurd to ask whether or not a zone in space is one’s own starship).
To avoid cluttering the fragment graph, the states of context nodes are not shown, contrary to what happens with input and resident nodes. This is mainly because they are Boolean nodes whose values are relevant only for deciding whether to use a resident random variable’s local distribution or its default distribution.
Probability Distributions
No probability values are shown for the states of the nodes of the fragment graph in Figure 8. This is because nodes in a fragment graph do not represent individual random variables with well-defined probability distributions. Instead, a node in an MFrag represents a generic class of random variables. To draw inferences or declare evidence, we must create instances of the random variable classes.
To find the probability distribution for an instance of DangerToSelf(s, t), the first step is to identify all instances of HarmPotential(st, t) and OpSpec(st) for which the context constraints are satisfied. If there are none, then the default distribution that assigns value Absurd with probability 1 must be used. Otherwise, to complete the definition of the Danger to Self MFrag, a local distribution must be specified for its lone resident node, DangerToSelf(s, t).
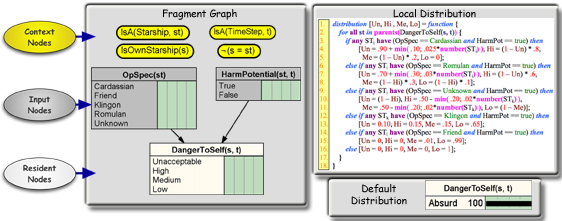
The pseudo-code on the right defines a local distribution for the danger to a starship due to all starships that influence its danger level. Local distributions in standard BNs are typically represented by static tables, which limits each node to a fixed number of parents. On the other hand, an instance of a node in an MTheory might have any number of parents. Thus, MEBN implementations (i.e. languages based on MEBN logic) must provide an expressive language for defining local distributions. In this work, the use of pseudo-code is intended to convey the idea of using local expressions to specify probability distributions, while not committing to a particular syntax.
Lines 3 to 5 cover the case in which there is at least one nearby starship operated by Cardassians and having the ability to harm the Enterprise. This is an uncomfortable situation for Capitan Picard, the Enterprise Commander, and his starship, where the probability of an unacceptable danger to self is 0.90 plus the minimum of 0.10 and the result of multiplying 0.025 by the total number of starships that are harmful and operated by Cardassians.
Also the remaining belief (i.e. the difference between 100% and the belief in state Unacceptable is divided between High (80% of the remainder) and Medium (20% of the remainder) whereas belief in Low is zero. The remaining lines use similar formulas to cover the other possible configurations in which there exist starships with potential to harm Enterprise (i.e. HarmPotential(st, t) = True). The last conditional statement of the local expression covers the case in which no nearby starships can inflict harm upon the Enterprise (i.e. all nodes HarmPotential(st, t) have value False). In this case, the value for DangerToSelf(s, t) is Low with probability 1.
Instantiating MFrags
 The graph on the left depicts an instantiation of the Danger To Self MFrag for which there are four starships nearby, three of them operated by Cardassians and one by the Romulans. Also, the Romulan and two of the Cardassian starships are within a range at which they can harm the Enterprise, whereas the other Cardassian starship is too far away to inflict any harm.
The graph on the left depicts an instantiation of the Danger To Self MFrag for which there are four starships nearby, three of them operated by Cardassians and one by the Romulans. Also, the Romulan and two of the Cardassian starships are within a range at which they can harm the Enterprise, whereas the other Cardassian starship is too far away to inflict any harm.
Following the procedure describing the DTS MFrag's distribution, the belief for state Unacceptable is .975 (.90 + .025*3) and the beliefs for states High, Medium, and Low are .02 ((1-.975)*.8), .005 ((1-.975)*.2), and zero respectively. In short, the pseudo-code covers all possible input node configurations by linking the danger level to the number of nearby starships that have the potential to harm our own starship. The formulas state that if there are any Cardassians or Romulan starships within Enterprise’s range, then a glimpse of what would the distribution for danger level given the number of nearby starships looks like is depicted in the table below.
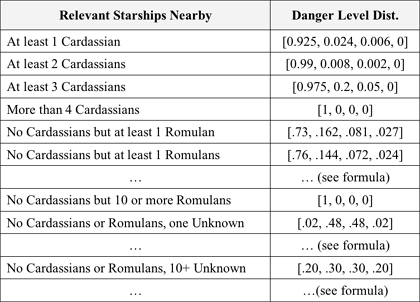 Following the same logic depicted in the formula, if there are only friendly starships nearby with the ability to harm the Enterprise, then the distribution becomes [0, 0, 0.01, .99]. The last line indicates that if that no starship can harm the Enterprise, then the danger level will be Low for sure. As noted previously, a powerful formalism is needed to represent complex scenarios at a reasonable level of fidelity. In the probability distribution shown in this example, additional detail could have been added and many nuances might have been explored. For example, a large number of nearby Romulan ships might have been considered as a fair indication of a coordinated attack and therefore implied greater danger than an isolated Cardassian ship.
Following the same logic depicted in the formula, if there are only friendly starships nearby with the ability to harm the Enterprise, then the distribution becomes [0, 0, 0.01, .99]. The last line indicates that if that no starship can harm the Enterprise, then the danger level will be Low for sure. As noted previously, a powerful formalism is needed to represent complex scenarios at a reasonable level of fidelity. In the probability distribution shown in this example, additional detail could have been added and many nuances might have been explored. For example, a large number of nearby Romulan ships might have been considered as a fair indication of a coordinated attack and therefore implied greater danger than an isolated Cardassian ship.
Nonetheless, this example was purposely kept simple in order to clarify the basic capabilities of the logic. It is clear that more complex knowledge patterns could be accommodated as needed to suit the requirements of the application. MEBN logic has built-in logical MFrags that provide the ability to express any sentence that can be expressed in first-order logic. Laskey (2005) proves that MEBN logic can implicitly express a probability distribution over interpretations of any consistent, finitely axiomatizable first-order theory. This provides MEBN with sufficient expressive power to represent virtually any scientific hypothesis.